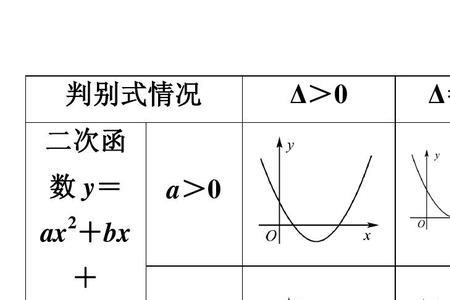
判别式小于0是没有实数根,但并不是说方程判别式小于0就没有根,方程判别式小于0的根为复数根。
判别式小于零,就不存在实根,更不用说有韦达定理了。也就是说,只有判别式大于等于零时,韦达定理才有意义。
根的判别式是判定方程是否有实根的充要条件,韦达定理说明了根与系数的关系。
无论方程有无实数根,实系数一元二次方程的根与系数之间适合韦达定理。
判别式小于0韦达定理意义
韦达定理是建立在一元二次方程在实数范围内有两个根的基础上的。
例如,aX2十bX十c=0这个一元二次方程,只有这个一元二次方程的判别式b2一4ac≥0时,这个一元二次方程在实数范围内才有两个根X1和X2。
根据韦达定理知,X1十x2=-b/a
X1xx2=c/a。
当这个一元二次方程的判别式小于零时,韦达定理不再有意义。