严格回答这个问题必须先严格定义什么是曲边图形的面积,这对于一般的平面点集不是个显然的概念,否则无从谈起精不精确。 以直角坐标系中的曲边梯形为例,先用测度定义什么是平面图形的面积以及什么是可求面积的图形,然后用Darboux上和与Darboux下和两边夹证明连续函数围出来的曲边梯形是可求面积的且面积恰好是inf{S}和sup{s},然后证明Darboux上(下)和的极限恰好是上(下)积分,然后因为连续函数一定可积所以上积分=下积分=定积分=面积

运用定积分求面积
原创 | 2022-10-19 17:19:24 |浏览:1.6万
猜你想问
-
 保卫黄河运用了哪两种卡农 《保卫黄河》 ,是一首轮唱、合唱歌曲,是人们最熟悉的一首。这里采用了“卡农”的 复调手法,其中第二、三遍的“轮唱”,也是“卡农”的手法,第七乐章《保卫黄河》是传唱...
保卫黄河运用了哪两种卡农 《保卫黄河》 ,是一首轮唱、合唱歌曲,是人们最熟悉的一首。这里采用了“卡农”的 复调手法,其中第二、三遍的“轮唱”,也是“卡农”的手法,第七乐章《保卫黄河》是传唱... -
 运动员射箭运用的物理原理 答:应用的物理原理是:1、势能与动能的转化;2、惯性。运动员搭箭拉弓,使弓具有弹性势能,运动员放手后,弓的弹性势能就转化为箭的动能,使箭离开弓时具有一定的速度。所以...
运动员射箭运用的物理原理 答:应用的物理原理是:1、势能与动能的转化;2、惯性。运动员搭箭拉弓,使弓具有弹性势能,运动员放手后,弓的弹性势能就转化为箭的动能,使箭离开弓时具有一定的速度。所以... -
 如何运用abc调节负面情绪 2、要解决负面情绪困扰,还要理解好“情绪ABC理论”所谓的情绪ABC理论是由美国心理学家埃利斯所创建,他认为激发事件A(activating event)只是引发情绪和行为后果C(conse...
如何运用abc调节负面情绪 2、要解决负面情绪困扰,还要理解好“情绪ABC理论”所谓的情绪ABC理论是由美国心理学家埃利斯所创建,他认为激发事件A(activating event)只是引发情绪和行为后果C(conse... -
 手机中的管理运用删除了怎么办 以iPhone 7为例,设置中的设备管理被删除后,可以通过安装描述文件后,复原设备管理。1、在手机桌面找到设置图标,点击打开该应用。2、在设置界面,找到通用选项。3、在通...
手机中的管理运用删除了怎么办 以iPhone 7为例,设置中的设备管理被删除后,可以通过安装描述文件后,复原设备管理。1、在手机桌面找到设置图标,点击打开该应用。2、在设置界面,找到通用选项。3、在通... -
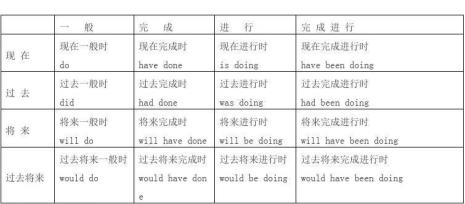 plan和hope在将来时态中如何运用 plan和hope,在将来时态当中表达的时候,一般都是要用一般现在时的结构。比如我打算明天去爬山,I plan to go climbing tomorrow。再比如,我希望你将来能成为一名医生,I...
plan和hope在将来时态中如何运用 plan和hope,在将来时态当中表达的时候,一般都是要用一般现在时的结构。比如我打算明天去爬山,I plan to go climbing tomorrow。再比如,我希望你将来能成为一名医生,I...
