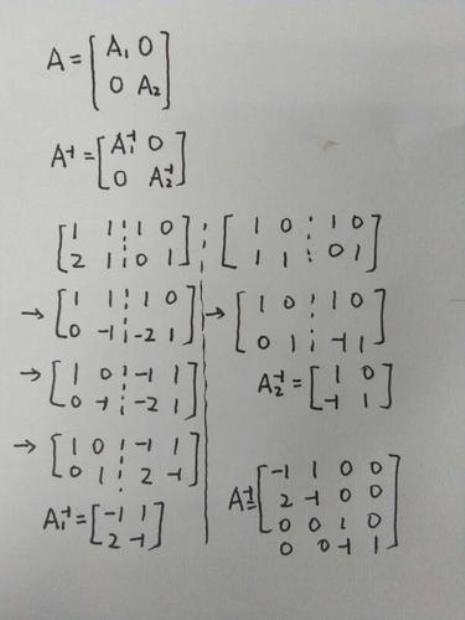
A1 0 … 0
0 A2 … 0
… … …
0 0 … Ak
和
A1^-1 0 … 0
0 A2^-1 … 0
… … …
0 0 … Ak^-1
相乘得到
E1 0 … 0
0 E2 … 0
… … …
0 0 … Ek
就可以证明了
如果一定要证明的话,证明四分块矩阵A
A1 0
0 A2
设A的逆矩阵为X
X1 X2
X3 X4
那么AX=E
A1 0 × X1 X2 =A1X1 A1X2 = E1 0
0 A2 X3 X4 A2X3 A2X4 0 E2
那么A1X1=E1 两边左乘A1^-1解得X1=A1^-1
A1X2=0 两边左乘A1^-1 X2=0
A2X3=0 两边左乘A2^-1 X3=0
A2X4=E2 两边左乘A2^-1 X4=A2^-1