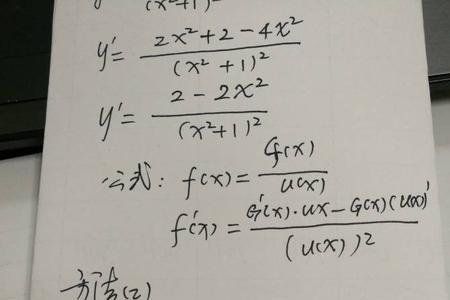1/x+1的导数

分之一的导数是什么

1+x分之一的导数是X分之一即X -1次方，它的导数就是-1*X^(-2)。

运用公式(u/v)'=(u'v-uv')/v²解[1/(x+1)]'

=[1'·(x+1)-1·(x+1)']/(x+1)²

=（0-1·1)/(x+1)²

=-1/(x+1)²

导函数：

如果函数y=f（x）在开区间内每一点都可导，就称函数f（x）在区间内可导。这时函数y=f（x）对于区间内的每一个确定的x值，都对应着一个确定的导数值，这就构成一个新的函数，称这个函数为原来函数y=f（x）的导函数，记作y'、f'（x）、dy/dx或df（x）/dx，简称导数。

几何意义函数y=f（x）在x0点的导数f'（x0）的几何意义：表示函数曲线在点P0（x0，f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）

1/x+1的导数

函数1/(x+1)的导数等于-1/(x+1)^2，在解决该问题时，首先要理解商的求导法则

(u/v)'=[u'v-uv']/v^2

其次要理解和函数的求导法则

(u+v)'=u'+v'

另外要记得基本求导公式

1'=0x'=1

在此基础上，即可求出函数1/(x+1)的导数为

[1/(x+1)]'

=[1'*(x+1)-1*(x+1)']/(x+1)^2

=-1/(x+1)^2

由此可见，函数1/(x+1)的导数等于-1/(x+1)^2

1/x+1的导数

1+x分之一的导数是[1/(1+x )]=-1/(x+1)^2*(1+x)=-1/(x+1)^2

扩展资料

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的.增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。