指数函数的图像规律

1、

由指数函数y=a^x与直线x=1相交于点(1，a)可知:在y轴右侧，图像从下到上相应的底数由小变大。

2、

由指数函数y=a^x与直线x=-1相交于点(-1，1/a)可知:在y轴左侧，图像从下到上相应的底数由大变小。

3、

指数函数的底数与图像间的关系可概括的记忆为:在y轴右边“底大图高”在y轴左边“底大图低”。。

4、

y=a的x次方与y=a分之1的x次方的图像关于y轴对称。

指数函数的图像规律

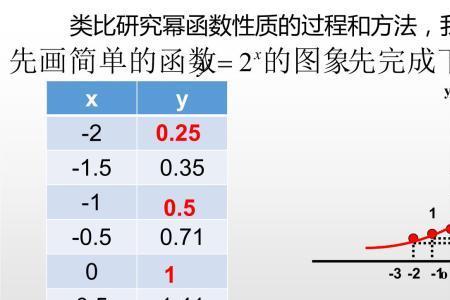
指数函数 y=a^x， a>0且a≠1

因为a^x>0， 所以指数函数的图像在x轴的上方 。

因为a^0=1，所以指数函数的图像都经过y轴上(0，1)点。

当a>1时，是增函数 ，从左到右图像是逐渐上升的 ，a的值越大 上升的越快 。

当a＜1时 ，是减函数 ，从左往右图像是逐渐下降的 ，a的值越小 下降的越快 。

函数 y=a^x 与 y=(1/a)^x的图像 关于y轴对称 。