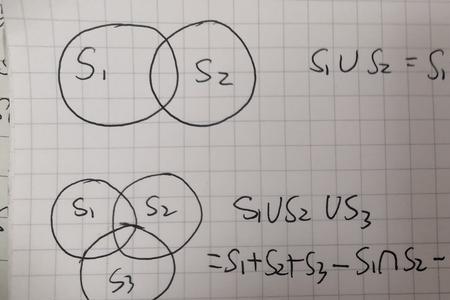
三者容斥最大值公式推导
若条件给出A∩B,A∩C,B∩C,A∩B∩C的值,对于全集I来说相当于整个集中所有部分之和,即I=A∪B∪C+D(D为非A非B非C的区域),那么这里面我们算得A∪B∪C需要把其A,B,C中重复的区域扣除,如果我们把A,B,C加在一起,其中对于A∩B(①+②)的区域是在A,B中各参与计算一次,需要减一个A∩B,同样的道理对于A∩C(①+③),B∩C(①+④)均需要减去一个,对于重复的A∩B∩C(①)在我们把A,B,C加和时计算了三次,在减去A∩B,A∩C,B∩C均包含①区域则又减去三次,要保证没有遗漏需要在加回一次A∩B∩C,则A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。
公式总结:A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。
I=A∪B∪C+D=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+D。