为什么两向量夹角为钝角条件

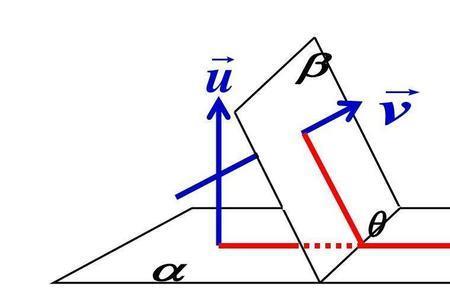
两向量夹角为钝角的条件是两亇向量的点积小于零。

两向量的点积等于这两个向量的模与这两个向量的夹角余弦的乘积。两向量的模恒大于零，当两向量夹角为钝角时，其余弦值小于零，从而两量的点积就小于零。另外，当两向量夹角为九十度（垂直）时，点积为零。当两向量来角为锐角时，点积大于零。

为什么两向量夹角为钝角条件

设两个向量是a=(x1，y1，z1)，b=(x2，y2，z2)，夹角是<向量a，向量b>

则向量的模：

|向量a|=√[(x1)^2+(y1)^2+(z1)^2]

|向量b|=√[(x2)^2+(y2)^2+(z2)^2]

因为两个向量夹角<向量a，向量b>的余弦

cos<向量a，向量b>=（向量a）•（向量b）/[|向量a||向量b|]

因为分母两向量模之积

[|向量a||向量b|]

=√[(x1)^2+(y1)^2+(z1)^2]√[(x2)^2+(y2)^2+(z2)^2]>0，是一个正数

两个向量夹角是钝角、即：180度<

<向量a，向量b>

>

90度

故

-1<

cos<向量a，向量b>

<0

因为

(向量a)•(向量b)

=

[|向量a||向量b|]cos<向量a，向量b>

=

=√[(x1)^2+(y1)^2+(z1)^2]√[(x2)^2+(y2)^2+(z2)^2]cos<向量a，向量b>=

=(x1，y1，z1)•(x2，y2，z2)

=

x1x2+y1y2+z1z2

所以若两向量a=(x1，y1，z1)，b=(x2，y2，z2)

的夹角为钝角，其条件必然是：

-

√[(x1)^2+(y1)^2+(z1)^2]√[(x2)^2+(y2)^2+(z2)^2]

<

x1x2+y1y2+z1z2

<

0。