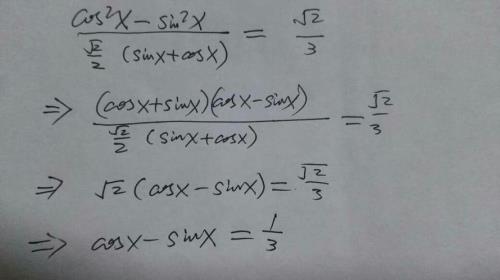sinx和cosx怎么换算

sinx和cosx之间的相互转化是通过诱导公式转化的

sin（π/2+x）=cosx  cos（π/2+x）=-sinx

sin（π/2-x）=cosx   cos（π/2-x）=sinx

奇变偶不变，符号看象限。通过这个口诀就可以轻松记住这些诱导公式。 

sinx和cosx怎么换算

可以用诱导公式进行换算。

sⅰnX=cos(π/2-Ⅹ)

cosX=sⅰn(π/2-x)

由正弦三函数的定义可以知道，一个角的正弦函数等于这个角的对边与斜边的比值，即sinα=y/r，当α换作π/2-α时，α角的对边就变成了π/2-α的邻边。

因此，sinX和cosX可以利用诱导公式相互转化。

sinx和cosx怎么换算

1、cosx和sinx的转换公式为：sinx=±√（1-cosx∧2），cosx=±√（1-sinx∧2），sin（π／2+x）＝cosx，cos（π／2+x）＝-sinx，（得出结论）

2、证明：sinx∧2+cosx∧2=1。三角函数是数学中属于初等函数中的超越函数的函数。（原因解释）

3.sinx与cosx之间的转换

三角函数公式

半角公式

sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)

cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)

tan(A/2)=√((1-cosA)/((1+cosA))

tan(A/2)=-√((1-cosA)/((1+cosA))

ctg(A/2)=√((1+cosA)/((1-cosA))

ctg(A/2)=-√((1+cosA)/((1-cosA))（内容延伸）