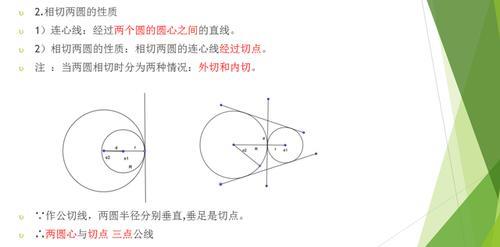
两圆相交必有两个交点证明
在同一平面内两圆的位置关系有内含(圆心距小于两圆半径差),内切(圆心距等于两半径差),相交,外切(圆心距等于两半径和)和外离(圆心距大于两半径和)。设两圆相交时圆心距d,则d大于两圆半径差,小于两圆半径和。两圆半径与圆心距构成三角形。由于圆是轴对称图形,则关于连心线必有对称三角形,也是两圆的公共点有两个,所以两圆相交必有两个交点。
两圆相交有两个交点如何证明
假设
半径为R的圆心为A,坐标为(x,y)
半径为S的圆心为B,坐标为(a,b)
两圆交点为C,D
AB与CD的交点为E,坐标为(X0,Y0)
过C点垂线与过E点水平线交点为F
令L为AB长度,K1为线AB的斜率,K2为线CD的斜率
则L=√[(a-x)²+(b-y)²]
K1=(b-y)/(a-x)
K2=-1/K1
CE²=R²-AE²
CE²=S²-EB²=S²-(AB-AE)²=S²-(L-AE)²=S²-L²-AE²+2LAE²
故AE=(R²-S²+L²)/2L
AE/L=(R²-S²+L²)/2L²
X0=x+(a-x)AE/L
=x+(a-x)(R²-S²+L²)/(2L²)
Y0=y+K1(X0-x)
R2=CE²= R²-(X0-x)²-(Y0-y)²
R2=CF²+EF²=(K2EF)²+EF²=(1+K2²)EF²
故EF=√[R2/(1+K2²)]
所以,C,D坐标计算公式为
Xc=X0-EF
=X0-√[R2/(1+K2²)]
Yc=Y0+K2(Xc-X0)
Xd=X0+EF
=X0+√[R2/(1+K2²)]
Yd=Y0+K2(Xd-X0)
两圆相交有两个交点如何证明
设交点连线为AB 则两圆心到A,B两点的距离分别相等 所以,两圆心的连线垂直平分AB 即 两圆相交,交点的连线与两圆心的连线互相垂直